This is a step-by-step intro to Random Forests using R, in particular using RStudio. RStudio is a powerful and open source integrated development environment (IDE) for R, available on Windows, Mac and Linux. It supports direct code excecution via a console, as well as an editor with code completion and other tools for plotting and managing your development workspace.
RStudio supports installation of all current available R packages hosted by the CRAN package repository.
I will provide instructions on how to install some basic packages required to start training a classifier and doing common data visualization.
Step 1: Install RStudio
To begin, Download an installer of RStudio for your OS, and follow the instructions. Installers for Supported Platforms can be found here:
* https://www.rstudio.com/products/rstudio/download/
Step 2: Gather some R packages
All R functions and datasets are stored in packages. In order to access a package functionality, it’s necessary to load it first. RStudio comes with a collection of packages pre-installed. To see this, start Rstudio and type on the console:
library() # You can also view your R version by typing: R.version
## _ ## platform x86_64-w64-mingw32 ## arch x86_64 ## os mingw32 ## system x86_64, mingw32 ## status ## major 2 ## minor 15.3 ## year 2013 ## month 03 ## day 01 ## svn rev 62090 ## language R ## version.string R version 2.15.3 (2013-03-01) ## nickname Security Blanket
To install additional packages, all you need is access to the internet and use install.packages() and update.packages() functions.
I will demonstrate how to build a Random forest classifier with Anderson’s Iris Data. So we need to get the following packages:
* caret (short for Classification And REgression Training)
* ggplot
* randomForest
install.packages("caret", libs_only = TRUE)
install.packages("ggplot2")
install.packages("randomForest")
# then load the libraries we just install library(caret) require(ggplot2) library(randomForest)
Step 3: Format the data
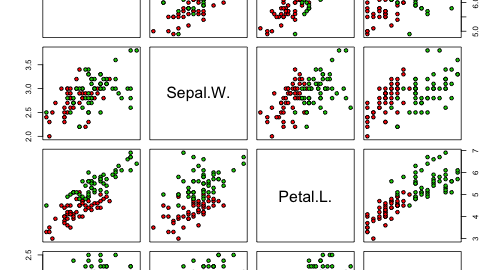
Fishers or Andersons) iris data set gives the measurements in centimeters of the variables sepal length and width and petal length and width, respectively, for 50 flowers from each of 3 species of iris. The species are Iris setosa, versicolor, and virginica.
The Iris data is available as part of the R Datasets Package, so no external data acquisition is needed.
# load the data iris = data.frame(iris) # simply format categorical variables as such iris$Species = as.factor(iris$Species) summary(iris)
## Sepal.Length Sepal.Width Petal.Length Petal.Width ## Min. :4.30 Min. :2.00 Min. :1.00 Min. :0.1 ## 1st Qu.:5.10 1st Qu.:2.80 1st Qu.:1.60 1st Qu.:0.3 ## Median :5.80 Median :3.00 Median :4.35 Median :1.3 ## Mean :5.84 Mean :3.06 Mean :3.76 Mean :1.2 ## 3rd Qu.:6.40 3rd Qu.:3.30 3rd Qu.:5.10 3rd Qu.:1.8 ## Max. :7.90 Max. :4.40 Max. :6.90 Max. :2.5 ## Species ## setosa :50 ## versicolor:50 ## virginica :50
Recursive Feature Elimination (RFE) via caret
The following will perform feature selection and random forest parameter tuning in a training set.
In caret, RFE consists on a resampling-based function. There are several arguments:
* x, a matrix or data frame of predictor variables
* y, a vector (numeric or factor) of outcomes
* sizes, a integer vector for the specific subset sizes that should be tested
rfeControl, a list of options that can be used to specify the model and the methods for prediction, ranking, resampling etc.
set.seed(2)
nvars = ncol(iris)-1
x = iris[c(1,2,3,4)]
y = iris$Species
subsets <- c(1:nvars)
ctrl <- rfeControl(functions = rfFuncs, # use Random Forest variable importance feature selection
method = "boot", # use bootstrap sampling
number = 50,
verbose = FALSE)
irisrfe <- rfe(x, y,
sizes = subsets,
rfeControl = ctrl)
print(irisrfe)
## Recursive feature selection ## ## Outer resampling method: Bootstrapped (50 reps) ## ## Resampling performance over subset size: ## ## Variables Accuracy Kappa AccuracySD KappaSD Selected ## 1 0.939 0.907 0.0333 0.0502 ## 2 0.959 0.938 0.0244 0.0367 * ## 3 0.958 0.936 0.0247 0.0372 ## 4 0.957 0.935 0.0236 0.0356 ## ## The top 2 variables (out of 2): ## Petal.Width, Petal.Length
To plot:
p <- ggplot(irisrfe$results, aes(x=irisrfe$results$Variables, y=irisrfe$results$Accuracy))
p + geom_line() + xlab("Number of subset variables") + ylab("Overall Accuracy (50 bootstraps)")
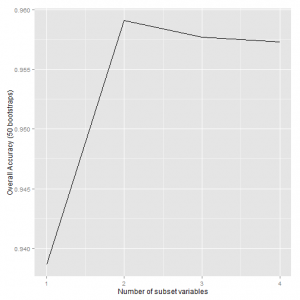
The results indicate that the best subset of features consists of 2 variables: Petal.Width, Petal.Length
However, this is for discriminating among 3 species of flowers, i.e we’re dealing with a muti-classification problem.
TO illustrate the basics of ROC curves it’s better to use a binary classification dataset. The iris dataset has 2 well separated classes (setosa vs. versicolor) and 2 classes with some overlap (versicolor vs. virginica)
First, subset the datasets:
# Iris binary classification, 4 features, 2 classes, n1=50/100, n2=50/100
# C1 = iris setosa, C2 = iris versicolor dataset iris3, datasets is the
# same as in iris but it's formatted differently 'Anderson's Iris Data --
# 2 species well separated classes'
irisdata1 = data.frame(rbind(iris3[, , 1], iris3[, , 2]), Species = rep(c("setosa",
"versicolor"), rep(50, 2)))
pairs(irisdata1[1:4], main = "Anderson's Iris Data -- 2 species well separated classes",
pch = 21, bg = c("red", "blue")[unclass(irisdata1$Species)])

# 'Anderson's Iris Data -- 2 species some overlaps in classes'
irisdata2 = data.frame(rbind(iris3[, , 2], iris3[, , 3]), Species = rep(c("versicolor",
"virginica"), rep(50, 2)))
pairs(irisdata2[1:4], main = "Anderson's Iris Data -- 2 species some overlaps in classes",
pch = 21, bg = c("red", "green3")[unclass(irisdata2$Species)])
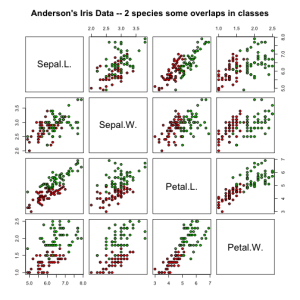
# we can run feature selection again in the subsetted dataset2 x = irisdata2[c(1:4)] y = irisdata2$Species irisrfe2 <- rfe(x, y, sizes = subsets, rfeControl = ctrl) print(irisrfe2)
## Recursive feature selection ## ## Outer resampling method: Bootstrapped (50 reps) ## ## Resampling performance over subset size: ## ## Variables Accuracy Kappa AccuracySD KappaSD Selected ## 1 0.903 0.805 0.0393 0.0791 ## 2 0.925 0.849 0.0418 0.0830 * ## 3 0.925 0.847 0.0403 0.0811 ## 4 0.925 0.848 0.0407 0.0820 ## ## The top 2 variables (out of 2): ## Petal.L., Petal.W.
# plot
p <- ggplot(irisrfe2$results, aes(x = irisrfe2$results$Variables, y = irisrfe2$results$Accuracy))
p + geom_line() + xlab("Number of subset variables") + ylab("Overall Accuracy (50 bootstraps)")
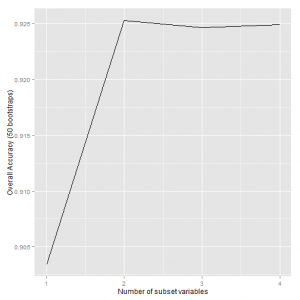
The next step is to used this subset of selected features to train the classifier. To do this, we need to tune the parameters of the classifier, in our case; we want to tune to the number of trees in the forest (ntree) and the number of variables to use at each split node (mtry)
# we start by leaving out independent test samples out of the data we are going to use to generate the model
# subset based on selected features
irisdata_sel = irisdata2[c("Petal.W.","Petal.L.","Species")]
set.seed(1)
inTrain <- createDataPartition(y = irisdata_sel$Species, ## the outcome data are needed
p = .75, ## The percentage of data in the training set
list = FALSE) ## The format of the results
# createDataPartition does a stratified random split of the data. To partition the data:
training <- irisdata_sel[ inTrain,]
testing <- irisdata_sel[-inTrain,]
# we'll use bootstrap samples of the data
bootControl <- trainControl(method = "boot",
number = 50, # number of boostrap iterations
savePredictions = TRUE,
p = 0.75, # % of data points of the training data sampled with replacement
classProbs = TRUE,
returnResamp = "all",
verbose = FALSE,
summaryFunction = twoClassSummary) # this allow us to obtain ROC metrics
# the caret package allow us to train the number of mtry variables, as following:
RFGrid <- expand.grid(.mtry=c(2:ncol(training)-1) )
RFfit <- train(Species ~ ., data = training,
method = "rf",
trControl = bootControl,
tuneGrid = RFGrid,
returnData = TRUE,
fitBest = TRUE,
verbose=FALSE,
metric="ROC")
## Loading required package: pROC
## Type 'citation("pROC")' for a citation.
##
## Attaching package: 'pROC'
##
## The following object(s) are masked from 'package:stats':
##
## cov, smooth, var
print(RFfit$finalModel)
## Call: ## randomForest(x = x, y = y, mtry = param$mtry, returnData = TRUE, fitBest = TRUE, verbose = FALSE) ## Type of random forest: classification ## Number of trees: 500 ## No. of variables tried at each split: 1 ## ## OOB estimate of error rate: 5.26% ## Confusion matrix: ## versicolor virginica class.error ## versicolor 36 2 0.05263 ## virginica 2 36 0.05263
The caret function train, has optimized our forest with ntree = 500 and mtry=2, and achieves a 6.58% out-of-bag (OOB) error.
Finally, we can asses our generalization error on the held-out test cases:
confusionMatrix(predict(RFfit, newdata = testing), testing$Species)
## Confusion Matrix and Statistics ## ## Reference ## Prediction versicolor virginica ## versicolor 11 0 ## virginica 1 12 ## ## Accuracy : 0.958 ## 95% CI : (0.789, 0.999) ## No Information Rate : 0.5 ## P-Value [Acc > NIR] : 1.49e-06 ## ## Kappa : 0.917 ## Mcnemar's Test P-Value : 1 ## ## Sensitivity : 0.917 ## Specificity : 1.000 ## Pos Pred Value : 1.000 ## Neg Pred Value : 0.923 ## Prevalence : 0.500 ## Detection Rate : 0.458 ## Detection Prevalence : 0.458 ## Balanced Accuracy : 0.958 ## ## 'Positive' Class : versicolor
# To do an ROC, we need the output probabilities of the classifier
# independent of the threshold used
outprob_train = predict(RFfit, newdata = training, type = "prob")
outprob_test = predict(RFfit, newdata = testing, type = "prob")
outprob_train$obs = training$Species
outprob_test$obs = testing$Species
ROCF_train <- plot.roc(outprob_train$obs, outprob_train$versicolor, col = "#000086",
lty = 1)
par(new = TRUE)
ROCF_test <- plot.roc(outprob_test$obs, outprob_test$versicolor, col = "#860000",
lty = 2, main = "ROC for mass max cvFolds")
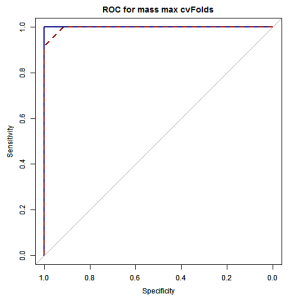
print(ROCF_train$auc) ## Area under the curve: 1 print(ROCF_test$auc) ## Area under the curve: 0.997
Our trained Random forest, achieves 95.8% overall accuracy on independent datasets. The AUC is 100% in the training set and 99.6% in the testset. This is a really great performance!
To have more control over the tuning parameters, we can use the Random Forest package directly and do a grid search or even build individual tress. To use the Random Forest package directly, i’ve created a simple function:
trainRF <- function(mtry, ntree, training, testing) {
experiment.rf <- randomForest(Species ~ ., data = training, importance = TRUE,
ntree = ntree, mtry = mtry, do.trace = FALSE, proximity = TRUE, keep.forest = TRUE)
# get oobError
oobError = as.numeric(experiment.rf$err.rate[ntree, 1])
# get missclassError
Trainresults = confusionMatrix(predict(experiment.rf, newdata = training),
training$Species)
Testresults = confusionMatrix(predict(experiment.rf, newdata = testing),
testing$Species)
TrainE = 1 - as.numeric(Trainresults$overall[1])
TestE = 1 - as.numeric(Testresults$overall[1])
output <- list(oobError = oobError, TrainE = TrainE, TestE = TestE)
return(output)
}
First test: look at varying Forest complexity (ntree) and (mtry)
# Design the grid search space
trainparam = expand.grid(mtry = c(1:2), ntree = c(10, seq(25, 250, 50), 500, 750, 1000))
gridsearch = data.frame()
# start the search
for (k in 1:nrow(trainparam)) {
aparam = trainparam[k, ]
RF_results = trainRF(aparam$mtry, aparam$ntree, training, testing)
gridsearch = rbind(gridsearch, c(aparam, RF_results))
}
# final results print(gridsearch) ## mtry ntree oobError TrainE TestE ## 2 1 10 0.05333 0.02632 0.04167 ## 21 2 10 0.06667 0.01316 0.04167 ## 3 3 10 0.06667 0.02632 0.04167 ## 4 4 10 0.05263 0.01316 0.04167 ## 5 1 25 0.06579 0.00000 0.04167 ## 6 2 25 0.06579 0.00000 0.04167 ## 7 3 25 0.06579 0.01316 0.04167 ## 8 4 25 0.05263 0.00000 0.04167 ## 9 1 75 0.06579 0.00000 0.04167 ## 10 2 75 0.06579 0.00000 0.04167 ## 11 3 75 0.06579 0.00000 0.04167 ## 12 4 75 0.06579 0.00000 0.04167 ## 13 1 125 0.06579 0.01316 0.04167 ## 14 2 125 0.06579 0.00000 0.04167 ## 15 3 125 0.06579 0.00000 0.04167 ## 16 4 125 0.06579 0.00000 0.04167 ## 17 1 175 0.05263 0.00000 0.04167 ## 18 2 175 0.06579 0.00000 0.04167 ## 19 3 175 0.06579 0.00000 0.04167 ## 20 4 175 0.05263 0.00000 0.04167 ## 211 1 225 0.06579 0.00000 0.04167 ## 22 2 225 0.05263 0.00000 0.04167 ## 23 3 225 0.06579 0.00000 0.04167 ## 24 4 225 0.06579 0.00000 0.04167 ## 25 1 500 0.05263 0.00000 0.04167 ## 26 2 500 0.05263 0.00000 0.04167 ## 27 3 500 0.06579 0.00000 0.04167 ## 28 4 500 0.06579 0.00000 0.04167 ## 29 1 750 0.05263 0.00000 0.04167 ## 30 2 750 0.06579 0.00000 0.04167 ## 31 3 750 0.06579 0.00000 0.04167 ## 32 4 750 0.06579 0.00000 0.04167 ## 33 1 1000 0.06579 0.00000 0.04167 ## 34 2 1000 0.06579 0.00000 0.04167 ## 35 3 1000 0.06579 0.00000 0.04167 ## 36 4 1000 0.06579 0.00000 0.04167
# Do some plots plot with color
trellis.par.set(caretTheme())
gridsearch$mtry <- as.factor(gridsearch$mtry)
# plot TrainError
p1 <- ggplot(gridsearch, aes(x = ntree, y = TrainE)) + geom_line(aes(colour = mtry)) +
scale_y_continuous(breaks = seq(0, max(gridsearch$TrainE), 0.01))
p1 + theme_bw() + theme(panel.grid.minor = element_line(colour = "grey", linetype = "dotted"))
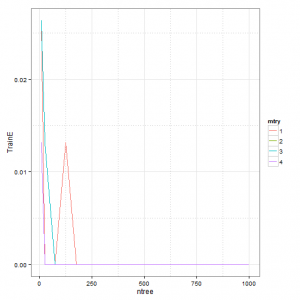
# plot TestError
p2 <- ggplot(gridsearch, aes(x = ntree, y = TestE)) + geom_line(aes(colour = mtry)) +
scale_y_continuous(breaks = seq(0, max(gridsearch$TestE), 0.05))
p2 + theme_bw() + theme(panel.grid.minor = element_line(colour = "grey", linetype = "dotted"))
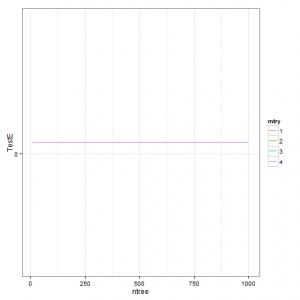
Final Remarks
This was intended to be a short tutorial in getting started with Random Forest in R. There is more you can do at the control level of the trees in R, but it was not demonstrated in this tutorial. Below are some useful links to further reading on the topics reviewed.
Some useful Links:
* For a graphical guide to getting-started with RStudio: http://dss.princeton.edu/training/RStudio101.pdf
* For a more detail tutorial on RFE and other topics visit http://topepo.github.io/caret/rfe.html
* To access ggplot2 documentation: http://docs.ggplot2.org/0.9.3/index.html
* Leo Breiman and Adele Cutler Random Forest website: http://www.stat.berkeley.edu/~breiman/RandomForests/cc_papers.htm