There are two different approaches to determining the conditional probabilities \(p(C_k|x)\). One technique is to model them directly, for example by representing them as parametric models and then optimizing the parameters using a training set. Alternatively, we can adopt a Bayesian approach in which we model the class-conditional densities given by \(p(x|C_k)\), together with the prior probabilities \(p(C_k)\) for the classes, and then we compute the required posterior probabilities using Bayes theorem \(p(C_k|x)= p(x|C_k)p(C_k)\)
In the simplest case, a model is linear in the input variables and therefore takes the form \(y(x)= w^Tx+w_0\), so that \(y\) is a real number. For classification problems, however, we wish to predict discrete class labels, or more generally posterior probabilities that lie in the range (0, 1). we transform the linear function of w using a nonlinear function f( · ) so that \(y(x)=f(w^Tx+w_0)\)
\(f( · )\) is known as an activation function. hence the decision surfaces are linear functions of x, even if the function f(·) is nonlinear. For this reason, these models are called generalized linear models.
Basis Functions
The simplest linear model for regression is one that involves a linear combination of the input variables
\(y(x,w)= w_0 +w_1x_1 +…+w_Dx_D\),
The key property of this model is that it is a linear function of the parameters \(w_0,…,w_D\). It is also a linear function of the input variables \(xi\).
We can extend this class of models by considering linear combinations of fixed nonlinear functions of the input variables, of the form \(φj(x)\) are known as basis functions.
if:
$$\phi =(\phi_0,…,\phi_{M−1})$$ and
$$w =(w_0,…,w_{M−1})$$
we can write the simplest linear classifier in matrix form as:
$$y(x)= w^Tx+w_0$$
The parameter \(w_0\) allows for any fixed offset in the data and is sometimes called a bias parameter or threshold.
An input vector x is assigned to class \(C1\) if \(y(x) = 0\) and to class \(C2\) otherwise.
Fisher’s linear discriminant
Considering a two-class problem in which there are $N1$ points of class \(C1\) and \(N2\) points of class \(C2\), so that the mean vectors of the two classes are \(m1 = average(N1)\) and \(m2 = average(N2)\)
The simplest measure of the separation of the classes, when projected onto \(w\), is the separation of the projected class means. This suggests that we might choose \(w\) so as to maximize
$$m2 − m1 = w^T(m2 −m1)$$
There’s a problem with this approach, two classes that are well separated in the original two-dimensional space \((x1,x2)\) but can have considerable overlap when projected onto the line joining their means. This difficulty arises from the strongly nondiagonal covariances of the class distributions.
The idea proposed by Fisher is to maximize a function that will give a large separation between the projected class means while also giving a small variance within each class, thereby minimizing the class overlap.
The Fisher criterion is defined to be the ratio of the between-class variance to the within-class variance and is given by
$$J(w) = (m2 − m1)^2/(s1^2 + s2^2)$$
The least-squares approach to the determination of a linear discriminant was based on the goal of making the model predictions as close as possible to a set of target values. By contrast, the Fisher criterion was derived by requiring maximum class separation in the output space.
Example: Anderson’s Iris Data
Dataset: (Fisher’s or Anderson’s) iris data set gives the measurements in centimeters of the variables sepal length and width and petal length and width, respectively, for 50 flowers from each of 3 species of iris. The species are Iris setosa, versicolor, and virginica.
Iris setosa
Iris versicolor:
Iris virginica:
Licensed under CC BY-SA 2.0 via Wikimedia Commons.
# Toy data: Iris binary classification, 4 features, 2 classes, n1=50/100, n2=50/100 # train: sample 0.75 of data # C1 = iris setosa, C2 = iris versicolor irisbin = subset(iris, Species=="setosa" | Species=="versicolor") set.seed(14102014) train <- sample(1:100, 75)
# "Anderson's Iris Data -- 2 species well separated classes"
irisdata = data.frame( rbind(iris3[,,1], iris3[,,2]), Species = rep(c("setosa","versicolor"), rep(50,2)))
pairs(irisdata[1:4], main = "Anderson's Iris Data -- 2 species well separated classes",
pch = 21, bg = c("red", "blue")[unclass(irisdata$Species)])

table(irisdata$Species[train])
## ## setosa versicolor ## 40 35
ldairis <- lda(Species ~ ., irisdata, subset = train) print(ldairis)
# Call: ## lda(Species ~ ., data = irisdata, subset = train) ## ## Prior probabilities of groups: ## setosa versicolor ## 0.5333333 0.4666667 ## ## Group means: ## Sepal.L. Sepal.W. Petal.L. Petal.W. ## setosa 4.990000 3.4025 1.480000 0.245000 ## versicolor 5.922857 2.7600 4.268571 1.328571 ## ## Coefficients of linear discriminants: ## LD1 ## Sepal.L. -0.3704904 ## Sepal.W. -1.5516582 ## Petal.L. 2.1819881 ## Petal.W. 2.5278116
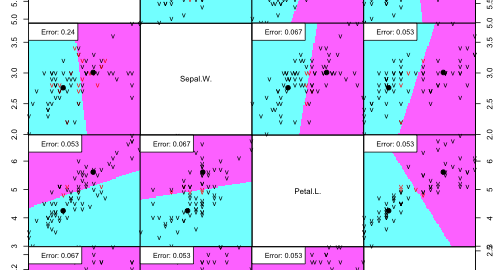
partimat(Species ~ ., data=irisdata, method="lda", subset=train, na.action="na.omit", plot.matrix=TRUE, print.err = 0.9)

Performance on train data:
confusionMatrix(predict(ldairis, irisdata[train,])$class, as.factor(irisdata[train,5]) )
## Confusion Matrix and Statistics ## ## Reference ## Prediction setosa versicolor ## setosa 40 0 ## versicolor 0 35 ## ## Accuracy : 1 ## 95% CI : (0.952, 1) ## No Information Rate : 0.5333 ## P-Value [Acc > NIR] : < 2.2e-16 ## ## Kappa : 1 ## Mcnemar's Test P-Value : NA ## ## Sensitivity : 1.0000 ## Specificity : 1.0000 ## Pos Pred Value : 1.0000 ## Neg Pred Value : 1.0000 ## Prevalence : 0.5333 ## Detection Rate : 0.5333 ## Detection Prevalence : 0.5333 ## Balanced Accuracy : 1.0000 ## ## 'Positive' Class : setosa ##
Performance on test data:
confusionMatrix(predict(ldairis, irisdata[-train,])$class, as.factor(irisdata[-train,5]) )
## Confusion Matrix and Statistics ## ## Reference ## Prediction setosa versicolor ## setosa 10 0 ## versicolor 0 15 ## ## Accuracy : 1 ## 95% CI : (0.8628, 1) ## No Information Rate : 0.6 ## P-Value [Acc > NIR] : 2.843e-06 ## ## Kappa : 1 ## Mcnemar's Test P-Value : NA ## ## Sensitivity : 1.0 ## Specificity : 1.0 ## Pos Pred Value : 1.0 ## Neg Pred Value : 1.0 ## Prevalence : 0.4 ## Detection Rate : 0.4 ## Detection Prevalence : 0.4 ## Balanced Accuracy : 1.0 ## ## 'Positive' Class : setosa ##
Since setosa and versicolor are so well separated in feature space, our linear discriminants have to problem is perfectly separating the classes.
Now if we look at versicolor and virginica, they produce a different feature set distribution:
# "Anderson's Iris Data -- 2 species some overlaps in classes"
irisdata = data.frame( rbind(iris3[,,2], iris3[,,3]), Species = rep(c("versicolor","virginica"), rep(50,2)))
pairs(irisdata[1:4], main = "Anderson's Iris Data -- 2 species some overlaps in classes",
pch = 21, bg = c("red", "green3")[unclass(irisdata$Species)])
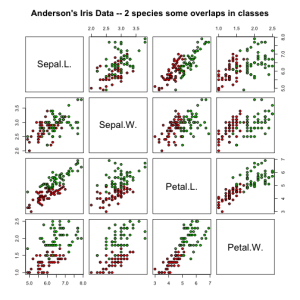
table(irisdata$Species[train]) ## ## versicolor virginica ## 40 35
ldairis <- lda(Species ~ ., irisdata, subset = train) print(ldairis)
## Call: ## lda(Species ~ ., data = irisdata, subset = train) ## ## Prior probabilities of groups: ## versicolor virginica ## 0.5333333 0.4666667 ## ## Group means: ## Sepal.L. Sepal.W. Petal.L. Petal.W. ## versicolor 5.8925 2.760000 4.250000 1.330000 ## virginica 6.6800 3.008571 5.611429 2.071429 ## ## Coefficients of linear discriminants: ## LD1 ## Sepal.L. -0.3898487 ## Sepal.W. -1.5466266 ## Petal.L. 1.2755075 ## Petal.W. 3.5679695
partimat(Species ~ ., data=irisdata, method="lda", subset=train, na.action="na.omit", plot.matrix=TRUE, print.err = 0.9)

Performance on train data:
confusionMatrix(predict(ldairis, irisdata[train,])$class, as.factor(irisdata[train,5]) )
## Confusion Matrix and Statistics ## ## Reference ## Prediction versicolor virginica ## versicolor 39 1 ## virginica 1 34 ## ## Accuracy : 0.9733 ## 95% CI : (0.907, 0.9968) ## No Information Rate : 0.5333 ## P-Value [Acc > NIR] : <2e-16 ## ## Kappa : 0.9464 ## Mcnemar's Test P-Value : 1 ## ## Sensitivity : 0.9750 ## Specificity : 0.9714 ## Pos Pred Value : 0.9750 ## Neg Pred Value : 0.9714 ## Prevalence : 0.5333 ## Detection Rate : 0.5200 ## Detection Prevalence : 0.5333 ## Balanced Accuracy : 0.9732 ## ## 'Positive' Class : versicolor ##
Performance on test data:
confusionMatrix(predict(ldairis, irisdata[-train,])$class, as.factor(irisdata[-train,5]) )
## Confusion Matrix and Statistics ## ## Reference ## Prediction versicolor virginica ## versicolor 10 0 ## virginica 0 15 ## ## Accuracy : 1 ## 95% CI : (0.8628, 1) ## No Information Rate : 0.6 ## P-Value [Acc > NIR] : 2.843e-06 ## ## Kappa : 1 ## Mcnemar's Test P-Value : NA ## ## Sensitivity : 1.0 ## Specificity : 1.0 ## Pos Pred Value : 1.0 ## Neg Pred Value : 1.0 ## Prevalence : 0.4 ## Detection Rate : 0.4 ## Detection Prevalence : 0.4 ## Balanced Accuracy : 1.0 ## ## 'Positive' Class : versicolor ##
Despite the feature distribution overlap, the LDA does a great job and produces very low error rates.
Quadratic Discriminant Analysis (QDA)
Unlike LDA, QDA Estimates the covariance matrix separately for each class \(k\).
Decision boundaries are quadratic equations in \(x\). QDA fits the data better than LDA, but has more parameters to estimate.
# "Anderson's Iris Data -- 2 species some overlaps in classes" qdairis <- qda(Species ~ ., irisdata, subset = train) print(qdairis)
## Call: ## qda(Species ~ ., data = irisdata, subset = train) ## ## Prior probabilities of groups: ## versicolor virginica ## 0.5333333 0.4666667 ## ## Group means: ## Sepal.L. Sepal.W. Petal.L. Petal.W. ## versicolor 5.8925 2.760000 4.250000 1.330000 ## virginica 6.6800 3.008571 5.611429 2.071429
partimat(Species ~ ., data=irisdata, method="qda", subset=train, na.action="na.omit", plot.matrix=TRUE, print.err = 0.9)

# performance on train data confusionMatrix(predict(qdairis, irisdata[train,])$class, as.factor(irisdata[train,5]) )
## Confusion Matrix and Statistics ## ## Reference ## Prediction versicolor virginica ## versicolor 38 1 ## virginica 2 34 ## ## Accuracy : 0.96 ## 95% CI : (0.8875, 0.9917) ## No Information Rate : 0.5333 ## P-Value [Acc > NIR] : <2e-16 ## ## Kappa : 0.9198 ## Mcnemar's Test P-Value : 1 ## ## Sensitivity : 0.9500 ## Specificity : 0.9714 ## Pos Pred Value : 0.9744 ## Neg Pred Value : 0.9444 ## Prevalence : 0.5333 ## Detection Rate : 0.5067 ## Detection Prevalence : 0.5200 ## Balanced Accuracy : 0.9607 ## ## 'Positive' Class : versicolor ##
# performance on test data confusionMatrix(predict(qdairis, irisdata[-train,])$class, as.factor(irisdata[-train,5]) )
## Confusion Matrix and Statistics ## ## Reference ## Prediction versicolor virginica ## versicolor 10 0 ## virginica 0 15 ## ## Accuracy : 1 ## 95% CI : (0.8628, 1) ## No Information Rate : 0.6 ## P-Value [Acc > NIR] : 2.843e-06 ## ## Kappa : 1 ## Mcnemar's Test P-Value : NA ## ## Sensitivity : 1.0 ## Specificity : 1.0 ## Pos Pred Value : 1.0 ## Neg Pred Value : 1.0 ## Prevalence : 0.4 ## Detection Rate : 0.4 ## Detection Prevalence : 0.4 ## Balanced Accuracy : 1.0 ## ## 'Positive' Class : versicolor ##
In this dataset, increasing the complexity of the classifier did not represent an improvement of the error rates (false positives and false negatives). Therefore, since you should always strive to keep the model with the lowest complexity that performs the best, we can propose that an LDA does just fine in classifying versicolor and virginica flowers using the petal and sepal length and petal.
For a Bayesian interpretation of discriminant analysis read another post here