Logistic regression is used for classification. Despite being called “regression”. It is useful when you are interested in predicting binary outcomes from a set of continuous predictor variables or features. Logistic regression is useful when the goal is to understand the role of the input variables in explaining the outcome.
Keeping our probabilistic view of classification, the posterior probability for class \(C_1\), using Bayes rule can be written as:
$$p(C_1|x) = \frac{p(x|C_1)p(C_1)}{p(x|C_1)p(C_1) + p(x|C_2)p(C_2)}$$
$$ = \frac{1}{1+exp(-a)}= \sigma(a) $$
where we have defined:
$$ a = log \frac{p(x|C_1)p(C_1)}{p(x|C_2)p(C_2)} $$
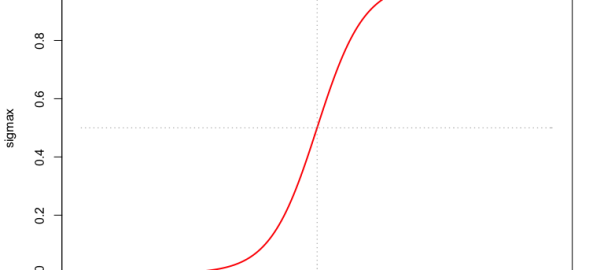
and \(\sigma(a)\) is the logistic sigmoid function. The term ‘sigmoid’ means S-shaped. The sigmoid function is also called a ‘squashing function’ because it maps the whole real axis into a finite interval between 0 and 1 (called the logit transformation). Logistic regression ensures that our estimate for conditional probability lies between 0 and 1.
# Plot of the logistic sigmoid function σ(a)
x = seq(from=-10, to=10, by=0.1)
sigmax = 1/(1+exp(-x))
plot(x=x, y=sigmax, type="l", col="red", lwd=2,
main="logistic sigmoid function sigma(x)")
lines(rep(0,length(sigmax)), sigmax, type="l", pch=1, col="darkgrey", lty=3)
lines(x, rep(0.5,length(x)), type="l", pch=1, col="darkgrey", lty=3)
In Logistic regression, the posterior probabilities of the \(K\) classes are model via linear functions in x. So we can write:
$$ p(C=k|X=x) = \frac{e^{\beta_{k0} + \beta_k^T(x)}}{1+ \sum_{l=1}^{K-1}e^{\beta_{k0} + \beta_k^T(x)}}$$
for \(k=1,…K-1\)
So for a binary classification problem, when \(K=2\)
$$p(C_1|x) = \frac{e^{\beta_0 + \beta_1^T(x)}}{1+e^{\beta_0 + \beta_1^T(x)}}$$
$$p(C_2|x) = 1-p(C_1|x)$$
Fitting Logistic Regression Models
Logistic regression models are usually fit by maximum likelihood estimation (MLE), in other words, by maximizing the conditional likelihood of a given class \(C\) given \(X\).
The likelihood gives us the probability of observing the data under our model assumption. So the goal of MLE is to find the model parameters that maximize the likelihood of the observed data with our model.
Using a simulated dataset of credit card default payment information on 1000 costumers. We have the following discrete and continues variables:
- student:
(discrete) with levels No and Yes indicating whether the customer is a student
- balance:
(continuos) The average balance that the customer has remaining on their credit card after making their monthly payment
- income:
(continuos) Income of customer
summary(Default)
## default student balance income ## No :9667 No :7056 Min. : 0.0 Min. : 772 ## Yes: 333 Yes:2944 1st Qu.: 481.7 1st Qu.:21340 ## Median : 823.6 Median :34553 ## Mean : 835.4 Mean :33517 ## 3rd Qu.:1166.3 3rd Qu.:43808 ## Max. :2654.3 Max. :73554
# let's look at the distribution of some variables
yes = Default[Default$default == "Yes",]
no = Default[Default$default == "No",]
colors = col = rainbow(2, alpha = 0.5)
xlimr = c(min(range(yes$balance), range(no$balance)), max(range(yes$balance),
range(no$balance)))
ylimr = c(min(range(yes$income), range(no$income)), max(range(yes$income), range(no$income)))
# plot
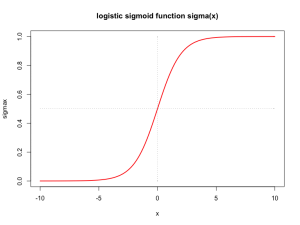
plot(yes$balance, yes$income, col = colors[1], pch = 0, xlim = xlimr, ylim = ylimr,
xlab = "balance", ylab = "income", cex = 0.6)
par(new = TRUE)
plot(no$balance, no$income, col = colors[2], pch = 1, xlim = xlimr, ylim = ylimr,
xlab = "balance", ylab = "income", cex = 0.6, main = "Default payment?")
legend("topright", legend = c("Yes", "No"), col = colors, pch = c(0, 1))
The goal is to predict which costumers will default in their credit card payments based on the information about their balance, income or student status.
Intuitively, if we only consider balance, a constumer with a higher balance is more likely to default (as can be seen in the plot above). With logistic regression we can build a predictor that captures this intuition represented in the data:
probDefault = glm(default~balance,family="binomial",data=Default) #family="binomial" is equivalent to logit function print(probDefault)
## ## Call: glm(formula = default ~ balance, family = "binomial", data = Default) ## ## Coefficients: ## (Intercept) balance ## -10.651331 0.005499 ## ## Degrees of Freedom: 9999 Total (i.e. Null); 9998 Residual ## Null Deviance: 2921 ## Residual Deviance: 1596 AIC: 1600
Once the model is fitted and parameters are optimized, we can make predictions with different feature values, for example:
What is the estimated probability that a costumer will default if their balance consists of $1000?
$$p(C_1|x) = \frac{exp^{\text{-10.6513 + 0.0055(1000)}}}{1+exp^{\text{-10.6513 + 0.0055(1000)}}} = $$
or
exp(as.numeric(probDefault$coefficients[1]) + as.numeric(probDefault$coefficients[2])*1000)/(1+exp(as.numeric(probDefault$coefficients[1]) + as.numeric(probDefault$coefficients[2])*1000))
## [1] 0.005752145
That’s approximately 6% probability that they will default. What if their balance consists of 3000?
or
exp(as.numeric(probDefault$coefficients[1]) + as.numeric(probDefault$coefficients[2])*3000)/(1+exp(as.numeric(probDefault$coefficients[1]) + as.numeric(probDefault$coefficients[2])*3000))
## [1] 0.9971152
What if they are a student or not?
probDefault = glm(default~student,family="binomial",data=Default) #family="binomial" is equivalent to logit function print(probDefault)
## ## Call: glm(formula = default ~ student, family = "binomial", data = Default) ## ## Coefficients: ## (Intercept) studentYes ## -3.5041 0.4049 ## ## Degrees of Freedom: 9999 Total (i.e. Null); 9998 Residual ## Null Deviance: 2921 ## Residual Deviance: 2909 AIC: 2913
if they are a student predictor1 = 1
or
exp(as.numeric(probDefault$coefficients[1]) + as.numeric(probDefault$coefficients[2])*1)/(1+exp(as.numeric(probDefault$coefficients[1]) + as.numeric(probDefault$coefficients[2])*1))
## [1] 0.04313859
if they are not a student predictor1 = 0
or
exp(as.numeric(probDefault$coefficients[1]) + as.numeric(probDefault$coefficients[2])*0)/(1+exp(as.numeric(probDefault$coefficients[1]) + as.numeric(probDefault$coefficients[2])*0))
## [1] 0.02919501
So the probability of defaulting payments is slightly higher for students than for non students. We can keep making predictons based on single variables, but we can get a better idea of the factors involved in a credit default if we combine multiple predictors in our model.
Now train a logistic regression model using multiple features:
probDefault = glm(default~balance+income+student,family="binomial",data=Default) #family="binomial" is equivalent to logit function print(probDefault)
## ## Call: glm(formula = default ~ balance + income + student, family = "binomial", ## data = Default) ## ## Coefficients: ## (Intercept) balance income studentYes ## -1.087e+01 5.737e-03 3.033e-06 -6.468e-01 ## ## Degrees of Freedom: 9999 Total (i.e. Null); 9996 Residual ## Null Deviance: 2921 ## Residual Deviance: 1572 AIC: 1580
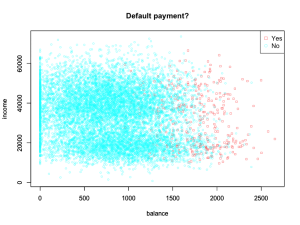
First, we notice that the coefficient for student is negative, while it was possitive before, and this change can be explained with confounding. It turns out that “student” and “balance” are confounding variables. Let’s look at the data to understand this:
balancebystudent = data.frame(balance=yes$balance) balancebystudent$isStudent = "Yes" balancenostudent = data.frame(balance=no$balance) balancenostudent$isStudent = "No" balance_student = rbind(balancebystudent,balancenostudent) summary(balance_student)
## balance isStudent ## Min. : 0.0 Length:10000 ## 1st Qu.: 481.7 Class :character ## Median : 823.6 Mode :character ## Mean : 835.4 ## 3rd Qu.:1166.3 ## Max. :2654.3
and let’s create boxplots of student and balance factors:
graph <- ggplot(balance_student, aes(isStudent, balance))
graph + geom_boxplot(aes(fill = factor(isStudent))) + xlab("Student status") + ylab("Credit card balance") + ggtitle("Default payment?")
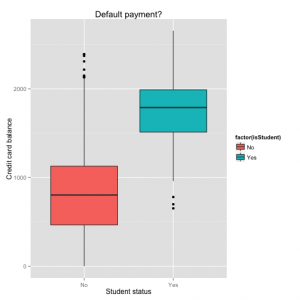
This shows that Students tend to have higher balances than non-students,
so the marginal default rate is higher than for non-students.
Now, let’s compute Default rates by balance levels for students and non-students
xlimYes = range(balancebystudent$balance)
yesdefRate = data.frame()
yesbalance = seq(from=xlimYes[1], to=xlimYes[2], by=100)
for(xbalance in yesbalance){
yesdefRate = rbind(yesdefRate, sum(balancebystudent$balance < xbalance)/nrow(balancebystudent))
}
xlimNo = range(balancenostudent$balance)
nodefRate = data.frame()
nobalance = seq(from=xlimNo[1], to=xlimNo[2], by=100)
for(xbalance in nobalance){
nodefRate = rbind(nodefRate, sum(balancenostudent$balance < xbalance)/nrow(balancenostudent))
}
# plot
colors = col = rainbow(2, alpha = 1)
xlimr = c(min(xlimYes, xlimNo), max(xlimYes, xlimNo))
# plot
plot(yesbalance, yesdefRate$X0, col = colors[1], type="p",
xlim = xlimr, ylim=c(0,1),
xlab = "balance", ylab = "Default Rate", cex = 0.8)
par(new = TRUE)
plot(nobalance, nodefRate$X0, col = colors[2], type="p",
xlim = xlimr, ylim=c(0,1),
xlab = "balance", ylab = "Default Rate", cex = 0.8)
legend("bottomright", legend = c("Student", "No student"), col = colors, pch=1)
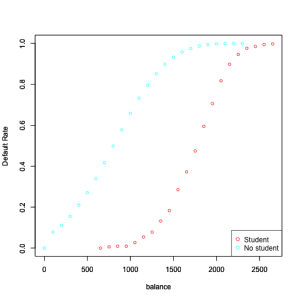
However, this shows that for a given level of balance, students default less that
non-students. Multiple logistic regression can tease this out, and this explains the negative sign in coefficient for student when we consider multiple descriptors.
Logistic regression on Iris dataset
Iris binary classification: Anderson’s Iris Data – 2 species with overlapping classes,
4 features, 2 classes, n1=50/100, n2=50/100
C1 = iris versicolor, C2 = iris virginica
Measured characteristics of the flowers include the width and the length of petals and sepals, in centimetres. The sepals consist of the outer parts of the flower, usually green and leaf-like, typically at the base of the flower enclosing the bud. For pictures of this datasets see a previous post here
irisdata = data.frame( rbind(iris3[,,2], iris3[,,3]), Species = rep(c("versicolor","virginica"), rep(50,2)))
# using the first measurement (Sepal length) and individual predictor of flower type
probSepalL = glm(Species~Sepal.L., family="binomial", data=irisdata)
print(probSepalL)
## ## Call: glm(formula = Species ~ Sepal.L., family = "binomial", data = irisdata) ## ## Coefficients: ## (Intercept) Sepal.L. ## -12.571 2.013 ## ## Degrees of Freedom: 99 Total (i.e. Null); 98 Residual ## Null Deviance: 138.6 ## Residual Deviance: 110.5 AIC: 114.5
probSepalLW = glm(Species~Sepal.L.+Sepal.W., family="binomial", data=irisdata) summary(probSepalLW)
## ## Call: ## glm(formula = Species ~ Sepal.L. + Sepal.W., family = "binomial", ## data = irisdata) ## ## Deviance Residuals: ## Min 1Q Median 3Q Max ## -1.87365 -0.89513 -0.05501 0.96084 2.35669 ## ## Coefficients: ## Estimate Std. Error z value Pr(>|z|) ## (Intercept) -13.0460 3.0974 -4.212 2.53e-05 *** ## Sepal.L. 1.9024 0.5169 3.680 0.000233 *** ## Sepal.W. 0.4047 0.8628 0.469 0.639077 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## (Dispersion parameter for binomial family taken to be 1) ## ## Null deviance: 138.63 on 99 degrees of freedom ## Residual deviance: 110.33 on 97 degrees of freedom ## AIC: 116.33 ## ## Number of Fisher Scoring iterations: 4
pairs(irisdata[1:4], main = "Iris Data - 2 species with some class overlap",
pch = 21, bg = c("red", "green3")[unclass(irisdata$Species)])
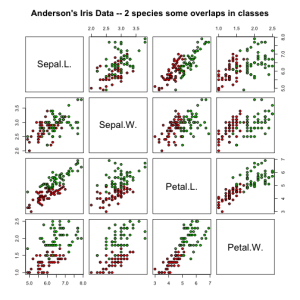
In general, with a classification model like logistic regression, we can extract probabilities for which the classifier predicts a flower is iris versicolor \(P(Y_i=versicolor|X_i)\) vs. iris virginica \(P(Y_i=virginica|X_i)\) based on the values of the predictors. In the last case, \(Xi=[Sepal.L,Sepal.W]\):
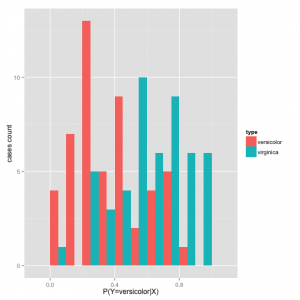
Plot a histogram of the data:
df=data.frame(pred=predict(probSepalLW, type = "response")) df$type = irisdata[,5] graph = ggplot(df, aes(x=pred, fill=type)) graph + geom_histogram(binwidth=.1, position="dodge") + labs(x="P(Y=versicolor|X)", y="cases count")
To turn this predictions probabilities into a classification, we choose a threshold to optimize either sensitivity, specificity or some other measure of optimal performance. Let \(Y\) represent the true flower type and \(\hat{Y}\) the predicted flower type:
* Sensitivity is defined as the fraction of versicolor flowers that are correctly classified as versicolor by our model $$P(\hat{Y}=versicolor|Y=versicolor)$$
* Specificity refers to the fraction of virginica flowers that are correctly classified as virginica by our model $$P(\hat{Y}=virginica|Y=virginica)$$
* Classification accuracy or correct classification rate is the overall proportion of correct predictions by the model.
Intuitively, we want all of this metrics to be maximal. In a perfect classification model, all of these metrics are 1, meaning that our model does not make any incorrect predictions. But no classifier is perfect and it will likely make some mistakes. So the goal of optimizing a prediction model is to choose a threshold such that we can maximize one or more of the above performance metrics.
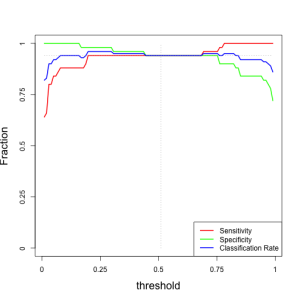
Here is a plot of metrics as a function of the decision threshold: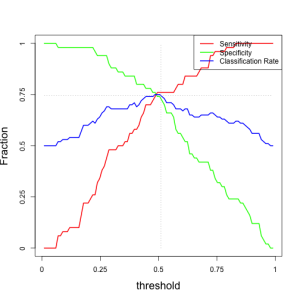
For our optimal threshold of 0.5, we have the following metrics:
metricsperf[ts>0.50 & ts<0.52,]
## [,1] [,2] [,3] ## [1,] 0.76 0.74 0.75 ## [2,] 0.76 0.72 0.74
However, if we look at the data plotted in pairs of features space, we can see that we have chosen predictors with great class overlap (not ideal). We can actually see that when feature values overlap, we get a decrease in prediction accuracy and this is confirmed with the insignificant p-values for the coefficients corresponding to sepal features:
logregmod = glm(Species~., family="binomial", data=irisdata) summary(logregmod)
## ## Call: ## glm(formula = Species ~ ., family = "binomial", data = irisdata) ## ## Deviance Residuals: ## Min 1Q Median 3Q Max ## -2.01105 -0.00541 -0.00001 0.00677 1.78065 ## ## Coefficients: ## Estimate Std. Error z value Pr(>|z|) ## (Intercept) -42.638 25.707 -1.659 0.0972 . ## Sepal.L. -2.465 2.394 -1.030 0.3032 ## Sepal.W. -6.681 4.480 -1.491 0.1359 ## Petal.L. 9.429 4.737 1.991 0.0465 * ## Petal.W. 18.286 9.743 1.877 0.0605 . ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## (Dispersion parameter for binomial family taken to be 1) ## ## Null deviance: 138.629 on 99 degrees of freedom ## Residual deviance: 11.899 on 95 degrees of freedom ## AIC: 21.899 ## ## Number of Fisher Scoring iterations: 10
Instead, we can choose Petal.L and Petal.W as a better choice of predictors:
probPetalLW = glm(Species~Petal.L.+Petal.W., family="binomial", data=irisdata) summary(probPetalLW)
#
# ## Call: ## glm(formula = Species ~ Petal.L. + Petal.W., family = "binomial", ## data = irisdata) ## ## Deviance Residuals: ## Min 1Q Median 3Q Max ## -1.73752 -0.04749 -0.00011 0.02274 1.89659 ## ## Coefficients: ## Estimate Std. Error z value Pr(>|z|) ## (Intercept) -45.272 13.610 -3.327 0.000879 *** ## Petal.L. 5.755 2.306 2.496 0.012565 * ## Petal.W. 10.447 3.755 2.782 0.005405 ** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## (Dispersion parameter for binomial family taken to be 1) ## ## Null deviance: 138.629 on 99 degrees of freedom ## Residual deviance: 20.564 on 97 degrees of freedom ## AIC: 26.564 ## ## Number of Fisher Scoring iterations: 8
Plotting the histogram of the prediction probabilities for each class:
df=data.frame(pred=predict(probPetalLW, type = "response")) df$type = irisdata[,5] graph = ggplot(df, aes(x=pred, fill=type)) graph + geom_histogram(binwidth=.1, position="dodge") + labs(x="P(Y=versicolor|X)", y="cases count")
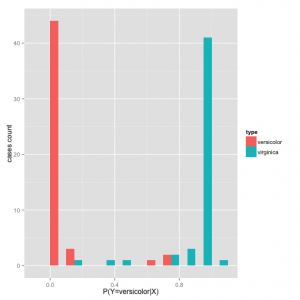
By the distribution of probabilities of the prediction, the class estimation is better separated into low probability for versicolor and high probability for virginica
This is the best performance classifier, since for a threshold of 0.5 (middle point between low and high probability) we have the following metrics:
metricsperf[ts>0.50 & ts<0.52,]
## [,1] [,2] [,3] ## [1,] 0.94 0.94 0.94 ## [2,] 0.94 0.94 0.94
Logistic Regression versus Linear Discriminant Analysis (LDA)
In a previous post, instead of logistic regression I illustrated the use of Linear Discriminant analysis – read here.
Logistic Regression and LDA are similar, The difference is in how the parameters are estimated:
* Logistic regression uses the conditional likelihood based on \(P(Y|X)\) (known as discriminative learning).
* LDA uses the full likelihood based on \(P(X,Y)\) (known as generative learning).
* Logistic regression is very popular for classification, especially when \(K = 2\).
* LDA is useful when n is small, or the classes are well separated, and Gaussian assumptions are reasonable. Also when \(K > 2\).
Considerations:
For an \(M\)-dimensional feature space, Logistic Regression has \(M\) adjustable parameters. By contrast, LDA via fitting Gaussian class conditional densities using maximum likelihood, requires \(2M\) parameters for the means and \(M(M +1)/2\) parameters for the (shared) covariance matrix. Together with the class prior \(p(C_1)\), this gives a total of \(M(M+5)/2+1\) parameters, which grows quadratically with \(M\). It is clear then that for large values of \(M\), there is an advantage in working with the logistic regression model instead of LDA.
LDA should only be used when Gaussian assumptions are reasonable. In our data, we can explore Gaussian assumptions in the distribution of features by testing for multivariate normality using Shapiro–Wilk test, or graphically with the Q-Q plot method. This will be a matter of a future post.